Global Optimization

Overview

Global optimization seeks the absolute minimum (or maximum) of an objective function over its entire feasible domain, even when the landscape contains multiple local optima, plateaus, and discontinuities. Unlike local optimization methods that converge to the nearest stationary point, global optimizers must systematically explore or intelligently sample the search space to identify the true global optimum. This challenge appears across diverse fields: molecular modeling (protein folding), machine learning (hyperparameter tuning), engineering design (structural optimization), and financial modeling (portfolio optimization with constraints).

The fundamental difficulty is that verifying a solution is globally optimal is generally intractable for non-convex problems. Most practical global optimization algorithms balance exploration (searching new regions) with exploitation (refining promising candidates) and can only guarantee convergence under specific smoothness or sampling conditions.

Implementation: These tools leverage SciPy, a mature scientific computing library that provides multiple global optimization algorithms. SciPy’s scipy.optimize module implements industry-standard methods suited for different problem structures, from simple univariate functions to complex multivariate landscapes. These algorithms range from gradient-free approaches (ideal for non-differentiable or discontinuous functions) to methods that exploit derivative information when available.

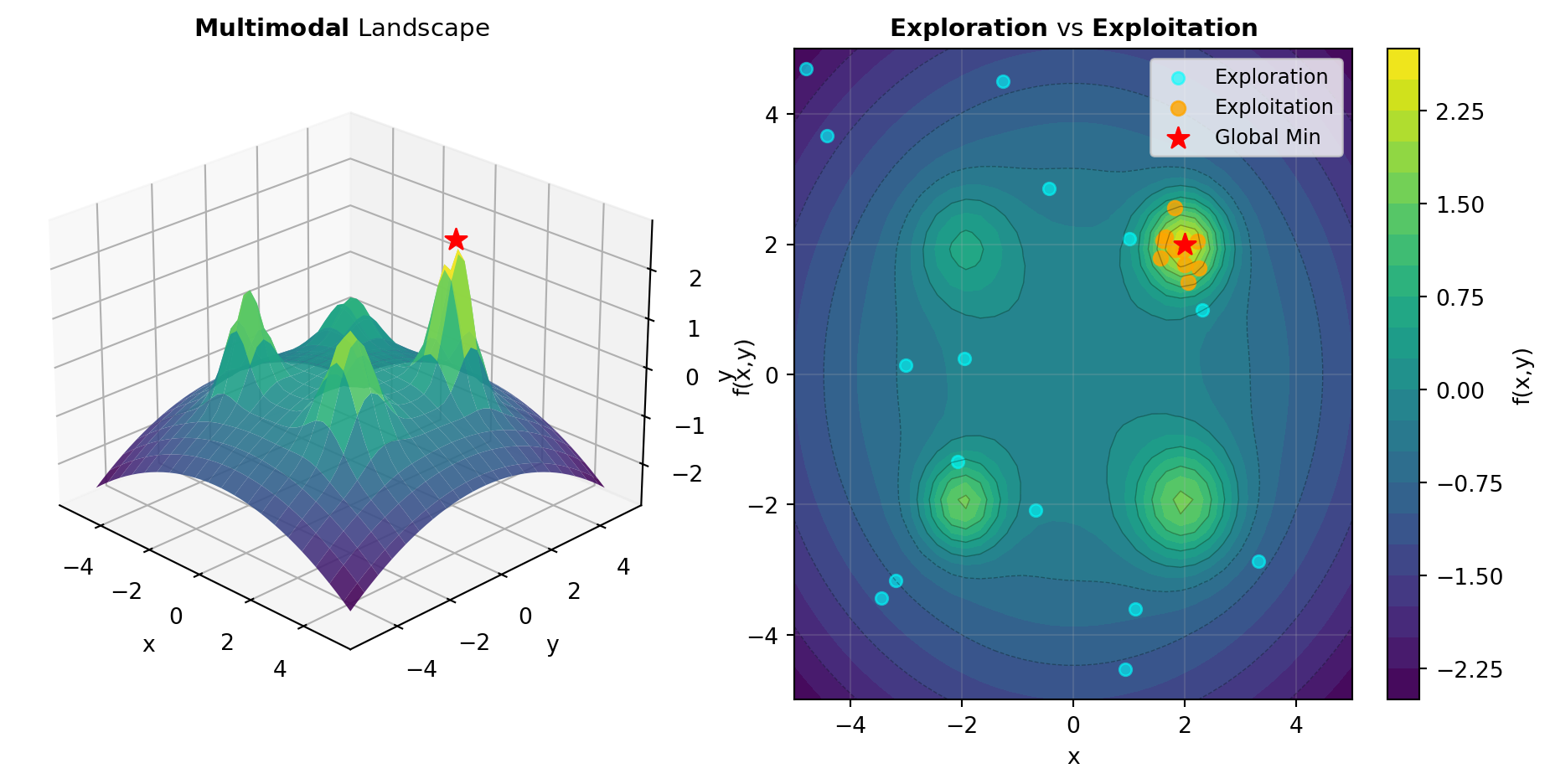
Search Space Landscape: Global optimization problems vary dramatically in complexity. The true challenge lies in whether the objective function exhibits convexity (single global optimum), multimodal structure (multiple local optima), or ruggedness (rapid fluctuations, discontinuities). The visualization below illustrates these landscape types and how different algorithms respond to them. Figure 1 shows a smooth multimodal surface alongside a discrete enumeration strategy.

Balancing Exploration and Exploitation: The core tension in global optimization is allocation of computational budget between discovering new promising regions (exploration) and refining candidate solutions in known regions (exploitation). Algorithms like DIFF_EVOLUTION use population-based search with mutation and recombination to explore broadly before focusing on elite solutions. In contrast, BASIN_HOPPING applies local optimization from random starting points and jumps across energy barriers. DUAL_ANNEALING uses temperature-based acceptance criteria to escape local traps, while BRUTE performs exhaustive grid enumeration for small-dimensional problems.

Problem Structure Awareness: Different algorithms excel for different problem characteristics. BRUTE is most effective for low-dimensional problems where grid enumeration is feasible, often serving as a baseline. DIFF_EVOLUTION is robust for continuous multimodal functions without derivative requirements, making it popular for scientific and engineering applications. BASIN_HOPPING works well when the problem has a clear “funnel” structure—many local optima separated by barriers. DUAL_ANNEALING provides a physics-inspired approach using simulated annealing principles with dual thermodynamic variables. SHGO (Simplicial Homology Global Optimization) uses sophisticated topological methods to guarantee convergence under smoothness assumptions, making it theoretically robust for smooth problems.

The choice of algorithm depends on problem properties: Is the function differentiable? Are gradient computations expensive? How many dimensions and local optima exist? What is the computational budget? Understanding these questions guides selection toward the most efficient method.

Figure 1: Global Optimization Landscapes and Solution Strategies: (A) A smooth multimodal function showing multiple local minima with a clear global optimum (red dot) at the bottom. (B) Illustration of how population-based and stochastic methods explore the landscape, discovering both local and global features.

Tools

Tool	Description
BASIN_HOPPING	Minimize a single-variable expression with SciPy’s basinhopping algorithm.
BRUTE	Perform a brute-force grid search to approximate the global minimum of a function.
DIFF_EVOLUTION	Minimize a multivariate function using differential evolution.
DUAL_ANNEALING	Minimize a multivariate function using dual annealing.
SHGO	Find global minimum using Simplicial Homology Global Optimization.