Assignment Problems
Overview
Assignment problems represent a fundamental class of combinatorial optimization where a set of agents (workers, machines, facilities) must be matched to a set of tasks (jobs, locations, resources) in a one-to-one manner that optimizes some measure of total cost or benefit. The mathematical elegance of these problems lies in their formulation as permutation optimization: finding the best way to reorder one set relative to another.
First studied systematically in the 1950s in operations research contexts, assignment problems have become ubiquitous in logistics, scheduling, resource allocation, and matching markets. The classic example involves assigning n workers to n jobs, where each worker has a different cost for performing each job, and the goal is to minimize total cost while ensuring each worker gets exactly one job and each job is performed by exactly one worker.
Problem Formulation: The assignment problem can be expressed as a discrete optimization problem with a cost matrix C where element C_{ij} represents the cost (or benefit, if negated) of assigning agent i to task j. The constraint matrix ensures that each agent is assigned to exactly one task and each task is assigned to exactly one agent. This structure makes assignment problems a special case of the transportation problem and the maximum weighted matching problem in bipartite graphs.
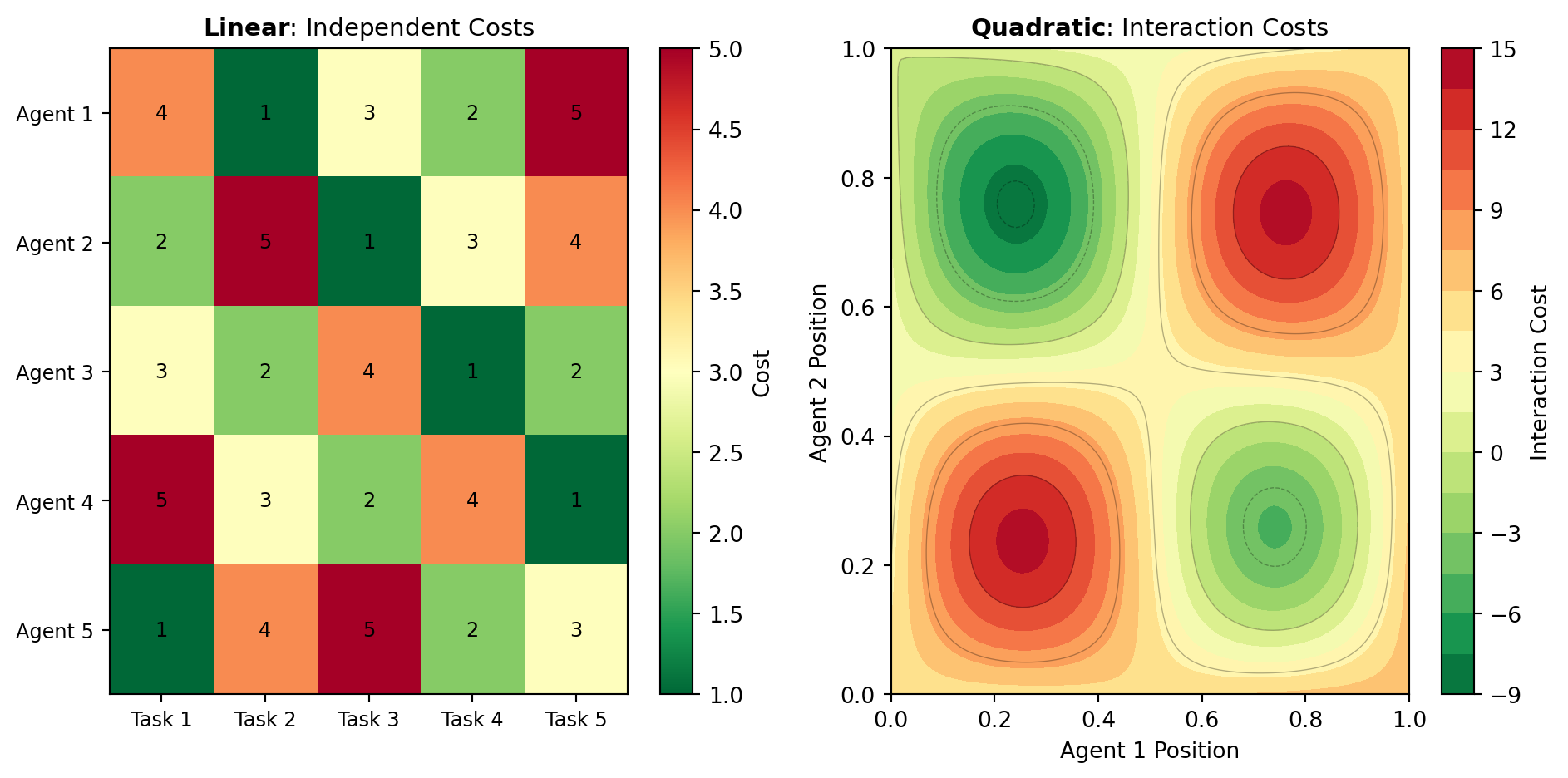
Linear vs. Quadratic Assignment: The linear assignment problem minimizes a sum of costs where each agent-task pair contributes independently to the total cost. This is one of the most efficiently solved combinatorial problems, with polynomial-time algorithms such as the Hungarian algorithm achieving solutions in O(n^3) time. The LINEAR_ASSIGNMENT tool leverages this efficiency through SciPy’s optimized implementation. In contrast, the quadratic assignment problem allows interaction terms where the cost of assigning agent i to task j depends on where other agents are assigned. This nonlinear dependency makes the quadratic variant significantly harder—in fact, NP-hard—but still tractable for moderate problem sizes. The QUAD_ASSIGN tool provides heuristic and exact methods for these more complex scenarios.
Implementation Considerations: These tools are built on SciPy and NumPy for efficient matrix operations and optimization. The linear assignment solver uses a combination of preprocessing and the Hungarian algorithm, while the quadratic solver employs sophisticated branch-and-bound or tabu search techniques. For very large problems, approximation algorithms and local search heuristics become necessary.
Applications and Use Cases: Assignment problems appear across numerous domains. In workforce planning, you assign workers to shifts or projects to minimize idle time or maximize skill utilization. In transportation and logistics, you match vehicles to delivery routes or facilities to demand centers. In manufacturing, you allocate production tasks to machines to minimize makespan or setup costs. In matching markets (job markets, housing allocation), you find stable or optimal assignments between two populations. The choice between linear and quadratic assignment depends on whether interactions between assignments matter: use linear assignment for independent cost structures, and quadratic assignment when placement of one agent affects the cost of placing another. Figure 1 illustrates how these two problem types differ in their cost structures.

Tools
| Tool | Description |
|---|---|
| LINEAR_ASSIGNMENT | Solve the linear assignment problem using scipy.optimize.linear_sum_assignment. |
| QUAD_ASSIGN | Solve a quadratic assignment problem using SciPy’s implementation. |