Drag
Overview
Drag is the resistance force exerted by a fluid on an object moving through it, or equivalently, by the fluid flowing past a stationary object. Understanding and quantifying drag is essential in chemical engineering for designing separators, settlers, fluidized beds, and particle transport systems, as well as in mechanical and aerospace engineering for vehicle design and fluid flow analysis. The drag force F_D is typically quantified by the drag coefficient C_D through the fundamental drag equation:
F_D = \frac{1}{2} \rho v^2 C_D A
where \rho is the fluid density, v is the relative velocity between the object and the fluid, and A is the reference area (typically the projected frontal area for spheres).
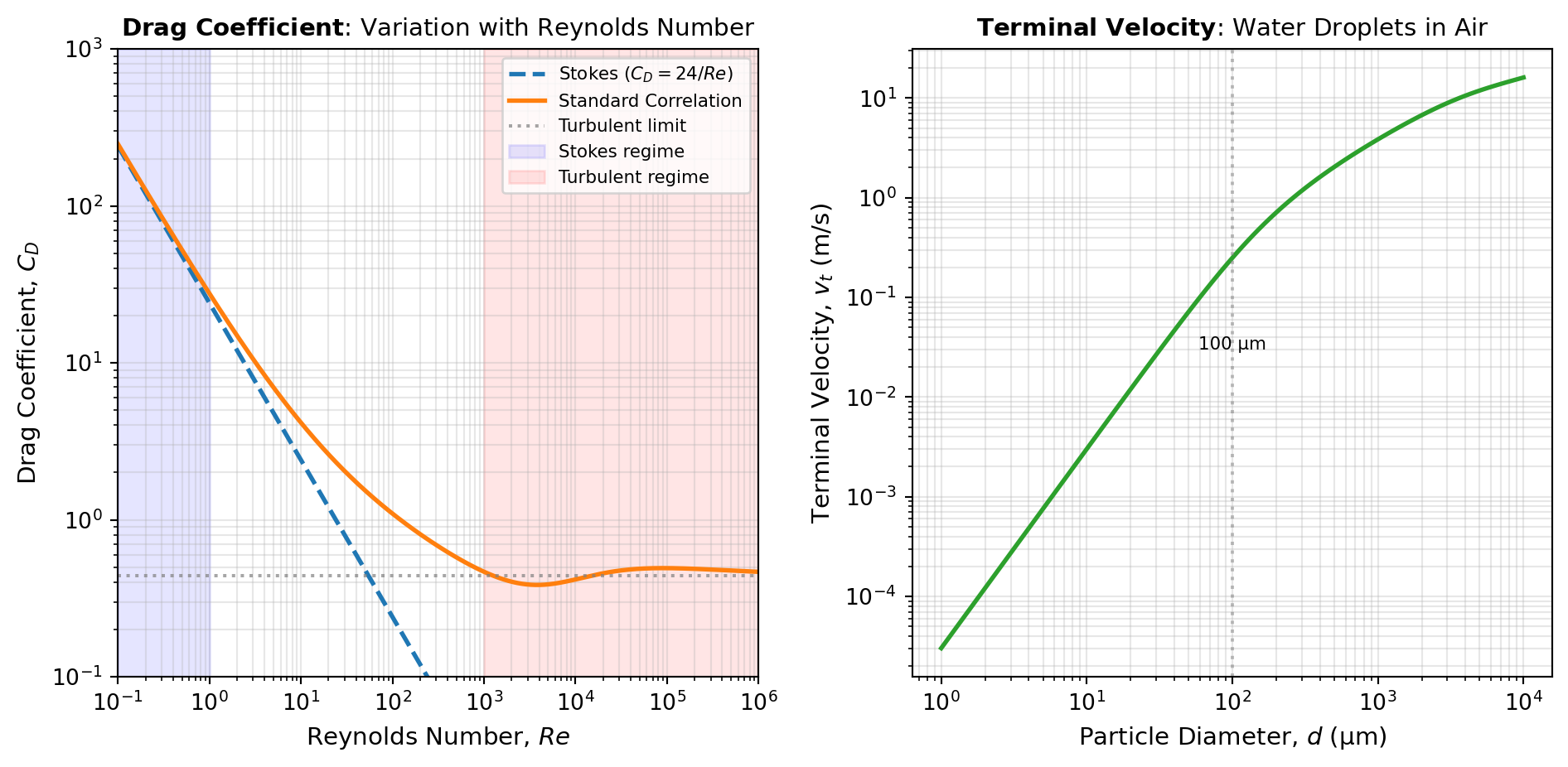
Drag Coefficient and Reynolds Number. The drag coefficient C_D is a dimensionless parameter that depends primarily on the Reynolds number Re = \rho v d / \mu, where d is the characteristic diameter and \mu is the dynamic viscosity. For spherical particles, the relationship between C_D and Re is complex and varies across different flow regimes. At very low Reynolds numbers (Re < 1), viscous forces dominate and Stokes’ law applies, giving C_D = 24/Re. As Re increases, the flow transitions through intermediate regimes where both viscous and inertial effects matter, and eventually reaches the turbulent regime (Re > 10^5) where C_D becomes nearly constant around 0.4-0.5 for smooth spheres.
Empirical Correlations. Because the drag coefficient cannot be expressed by a single analytical formula across all Reynolds numbers, numerous researchers have developed empirical correlations to fit experimental data. These correlations vary in their range of validity, accuracy, and mathematical form. The Stokes correlation (CD_STOKES) is accurate only for Re < 1, while correlations like Morsi-Alexander and Haider-Levenspiel cover wide Reynolds number ranges using piecewise or composite expressions. Mid-range correlations such as Cheng, Clift, and Swamee-Ojha provide good accuracy for typical engineering applications. Some correlations like Barati and Barati High-Re are specialized for specific Reynolds number ranges, with the high-Re version valid up to Re = 10^6.
Terminal Velocity Applications. A critical application of drag calculations is determining the terminal velocity of falling particles, where the drag force balances the gravitational force. The V_TERMINAL tool solves this balance iteratively using various drag coefficient correlations. For time-dependent motion, SPHERE_VEL_AT_T calculates instantaneous velocity and SPHERE_FALL_DIST determines the distance traveled. The TIME_V_TERMINAL tool specifically calculates how long it takes a particle in the Stokes regime to approach its terminal velocity, which is important for understanding transient behavior in separators.
Choosing the Right Correlation. Selecting an appropriate correlation depends on the Reynolds number range, required accuracy, and computational efficiency. For general-purpose calculations, the DRAG_SPHERE tool automatically selects the most appropriate correlation based on the Reynolds number. For specific applications, individual correlation tools offer control over the mathematical method used. The Morsi-Alexander and Haider-Levenspiel correlations are popular for computational fluid dynamics due to their wide validity range. For educational purposes or simple Stokes-regime calculations, CD_STOKES provides the clearest physical interpretation.
Implementation. All drag calculations are implemented using NumPy for numerical operations and SciPy for iterative solution of implicit equations when calculating terminal velocity. The correlations are based on empirical fits to experimental data and theoretical analysis published in peer-reviewed fluid mechanics and chemical engineering literature.

Tools
| Tool | Description |
|---|---|
| CD_ALMEDEIJ | Calculate drag coefficient of a sphere using the Almedeij correlation. |
| CD_BARATI | Calculate drag coefficient of a sphere using the Barati correlation. |
| CD_BARATI_HIGH | Calculate drag coefficient of a sphere using the Barati high-Re correlation (valid to Re=1E6). |
| CD_CEYLAN | Calculate drag coefficient of a sphere using the Ceylan correlation. |
| CD_CHENG | Calculate drag coefficient of a sphere using the Cheng correlation. |
| CD_CLIFT | Calculate drag coefficient of a sphere using the Clift correlation. |
| CD_CLIFT_GAUVIN | Calculate drag coefficient of a sphere using the Clift-Gauvin correlation. |
| CD_ENGELUND | Calculate drag coefficient of a sphere using the Engelund-Hansen correlation. |
| CD_FLEMMER_BANKS | Calculate drag coefficient of a sphere using the Flemmer-Banks correlation. |
| CD_GRAF | Calculate drag coefficient of a sphere using the Graf correlation. |
| CD_HAIDER_LEV | Calculate drag coefficient of a sphere using the Haider-Levenspiel correlation. |
| CD_KHAN_RICH | Calculate drag coefficient of a sphere using the Khan-Richardson correlation. |
| CD_MIKHAILOV | Calculate drag coefficient of a sphere using the Mikhailov-Freire correlation. |
| CD_MORRISON | Calculate drag coefficient of a sphere using the Morrison correlation. |
| CD_MORSI_ALEX | Calculate drag coefficient of a sphere using the Morsi-Alexander correlation. |
| CD_ROUSE | Calculate drag coefficient of a sphere using the Rouse correlation. |
| CD_SONG_XU | Calculate drag coefficient of a particle using the Song-Xu correlation for spherical and non-spherical particles. |
| CD_STOKES | Calculate drag coefficient of a sphere using Stokes law (Cd = 24/Re). |
| CD_SWAMEE_OJHA | Calculate drag coefficient of a sphere using the Swamee-Ojha correlation. |
| CD_TERFOUS | Calculate drag coefficient of a sphere using the Terfous correlation. |
| CD_YEN | Calculate drag coefficient of a sphere using the Yen correlation. |
| DRAG_SPHERE | Calculate the drag coefficient of a sphere using various correlations based on Reynolds number. |
| SPHERE_FALL_DIST | Calculate distance traveled by a falling sphere after a given time. |
| SPHERE_VEL_AT_T | Calculate the velocity of a falling sphere after a given time. |
| TIME_V_TERMINAL | Calculate time for a particle in Stokes regime to reach terminal velocity. |
| V_TERMINAL | Calculate terminal velocity of a falling sphere using drag coefficient correlations. |