Dimensionless

Overview

Dimensionless numbers are fundamental tools in fluid mechanics and engineering that characterize the relative importance of different physical forces and phenomena. By combining variables such as velocity, length scale, fluid properties, and forces into ratios, dimensionless numbers eliminate units and reveal the underlying physics governing fluid behavior. This enables engineers to compare vastly different systems, scale experimental results, predict flow regimes, and simplify complex partial differential equations into universal forms.

The power of dimensionless analysis lies in the Buckingham π theorem, which demonstrates that any physical relationship can be expressed in terms of dimensionless groups. This foundation enables dimensional analysis, scaling laws, and similarity theory—cornerstones of experimental fluid mechanics, process design, and computational validation.

Implementation: These tools leverage the fluids Python library, which provides validated implementations of dimensionless number calculations across fluid mechanics, heat transfer, and multiphase flow. Each tool wraps a fluids.core function with consistent parameter interfaces and automatic unit handling.

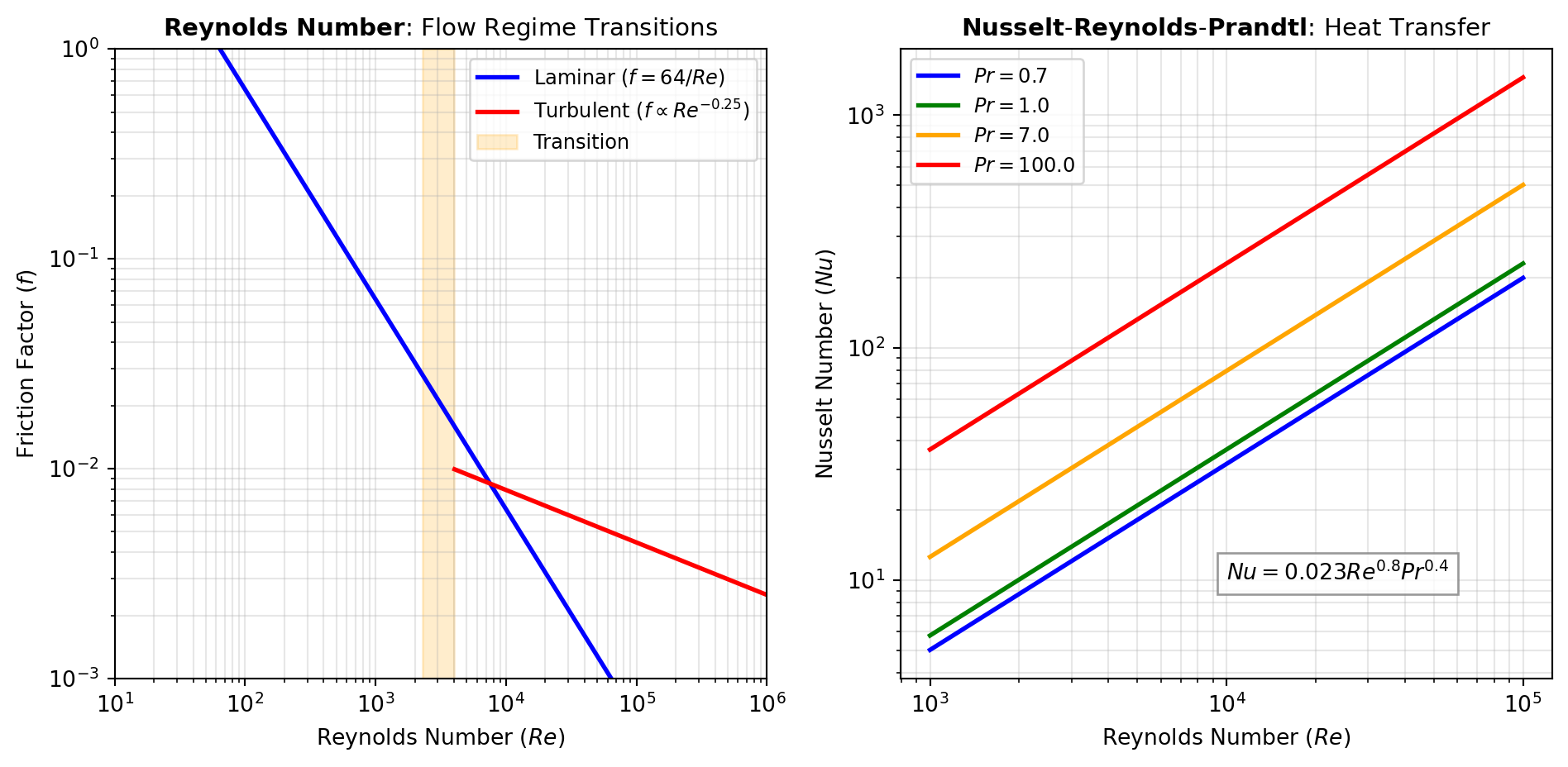
Flow Regime Numbers: Several dimensionless numbers classify flow behavior and predict regime transitions. The REYNOLDS number (Re = \rho V L / \mu) distinguishes laminar from turbulent flow, with critical values around 2300 for pipe flow. The FROUDE number (Fr = V / \sqrt{g L}) compares inertial to gravitational forces, critical for free-surface flows like open channels and ship hydrodynamics. The MACH number (Ma = V / c) compares flow velocity to sound speed, delineating subsonic, transonic, and supersonic regimes. Use these numbers to predict whether viscous, gravitational, or compressibility effects dominate.

Pressure and Force Ratios: The EULER number (Eu = \Delta p / (\rho V^2)) quantifies pressure drop relative to dynamic pressure, essential for pump and valve design. The DRAG coefficient (C_D) normalizes drag force, enabling comparison across different geometries and Reynolds numbers. The CAVITATION number (Ca = (p - p_v) / (0.5 \rho V^2)) assesses the risk of vapor bubble formation in low-pressure regions.

Surface Tension and Interfacial Flows: When surface tension dominates, the WEBER number (We = \rho V^2 L / \sigma) compares inertial to surface tension forces, critical for droplet breakup, atomization, and coating flows. The CAPILLARY number (Ca = \mu V / \sigma) balances viscous to surface tension forces, governing bubble dynamics and microfluidics. The BOND number (Bo = (\rho_L - \rho_G) g L^2 / \sigma) compares gravitational to surface tension forces, determining bubble shape and pool boiling regimes.

Heat Transfer Numbers: The NUSSELT number (Nu = h L / k) represents the ratio of convective to conductive heat transfer. Correlations typically express Nu as functions of REYNOLDS and PRANDTL numbers (Pr = \mu c_p / k), enabling prediction of heat transfer coefficients from flow conditions. The PECLET_HEAT number (Pe = Re \cdot Pr) characterizes the relative importance of advection to diffusion. For transient heat transfer, the FOURIER_HEAT number (Fo = \alpha t / L^2) measures thermal penetration depth.

Mass Transfer Numbers: Analogous to heat transfer, the SHERWOOD number (Sh = k_c L / D_{AB}) quantifies convective to diffusive mass transfer. The SCHMIDT number (Sc = \mu / (\rho D_{AB})) is the mass-transfer analog of the Prandtl number. The PECLET_MASS number (Pe = Re \cdot Sc) compares advection to diffusion, while FOURIER_MASS governs transient diffusion.

Multiphase and Buoyancy-Driven Flows: The GRASHOF number (Gr = g \beta \Delta T L^3 / \nu^2) drives natural convection, comparing buoyancy to viscous forces. The RAYLEIGH number (Ra = Gr \cdot Pr) determines convection onset in heated cavities. For particle-laden flows, the ARCHIMEDES number (Ar = g L^3 \rho_f (\rho_p - \rho_f) / \mu^2) characterizes particle settling. The CONFINEMENT number governs two-phase flow patterns in microchannels. Figure 1 illustrates how Reynolds and Froude numbers delineate flow regimes.

Figure 1: Dimensionless Number Regimes: (A) Reynolds number distinguishes laminar, transitional, and turbulent flow regimes. (B) Nusselt-Reynolds-Prandtl correlation for forced convection heat transfer, demonstrating how dimensionless groups collapse data onto universal curves.

Tools

Tool	Description
ARCHIMEDES	Calculate the Archimedes number (Ar) for a fluid and particle.
BEJAN	Compute the Bejan number (length-based or permeability-based).
BIOT	Calculate the Biot number for heat transfer.
BOILING	Calculate the Boiling number (Bg), a dimensionless number for boiling heat transfer.
BOND	Calculate the Bond number (Bo), also known as the Eötvös number (Eo).
CAPILLARY	Calculate the Capillary number (Ca) for a fluid system using fluids.core.Capillary.
CAVITATION	Calculate the Cavitation number (Ca) for a flowing fluid.
CONFINEMENT	Calculate the Confinement number (Co) for two-phase flow in a channel.
DEAN	Calculate the Dean number (De) for flow in a curved pipe or channel.
DRAG	Calculate the drag coefficient (dimensionless) for an object in a fluid.
ECKERT	Calculate the Eckert number using fluids.core.Eckert.
EULER	Calculate the Euler number (Eu) for a fluid flow.
FOURIER_HEAT	Calculate the Fourier number for heat transfer.
FOURIER_MASS	Calculate the Fourier number for mass transfer (Fo).
FROUDE	Calculate the Froude number (Fr) for a given velocity, length, and gravity.
FROUDE_DENSIMETRIC	Calculate the densimetric Froude number.
GRAETZ_HEAT	Calculate the Graetz number.
GRASHOF	Calculate the Grashof number.
HAGEN	Calculate the Hagen number.
JAKOB	Calculate the Jakob number for boiling fluid.
KNUDSEN	Calculate the Knudsen number.
LEWIS	Calculate the Lewis number.
MACH	Calculate the Mach number.
MORTON	Calculate the Morton number.
NUSSELT	Calculate the Nusselt number.
OHNESORGE	Calculate the Ohnesorge number.
PECLET_HEAT	Calculate the Peclet number for heat transfer.
PECLET_MASS	Calculate the Peclet number for mass transfer.
POWER_NUMBER	Calculate the Power number for an agitator.
PRANDTL	Calculate the Prandtl number.
RAYLEIGH	Calculate the Rayleigh number.
RELATIVE_ROUGHNESS	Calculate the relative roughness.
REYNOLDS	Calculate the Reynolds number.
SCHMIDT	Calculate the Schmidt number.
SHERWOOD	Calculate the Sherwood number.
STANTON	Calculate the Stanton number.
STOKES_NUMBER	Calculate the Stokes number.
STROUHAL	Calculate the Strouhal number.
SURATMAN	Calculate the Suratman number.
WEBER	Calculate the Weber number.