Compressible
Overview
Compressible flow describes fluid motion where density changes are significant—typically when gas velocities approach or exceed the speed of sound. Unlike incompressible flow where density remains constant, compressible flow exhibits complex coupling between velocity, pressure, temperature, and density through thermodynamic relationships. This behavior dominates in high-speed aerodynamics, gas pipeline networks, turbomachinery, and rocket nozzles.
The defining characteristic of compressible flow is the Mach number, M = V/c, where V is flow velocity and c is the local speed of sound. When M < 0.3, density changes remain below 5% and incompressible assumptions suffice. As Mach number increases, compressibility effects intensify: shock waves form, flow can become choked (reaching sonic conditions), and thermodynamic processes dictate pressure-temperature relationships.
Implementation: These tools leverage thermodynamic calculations through SciPy for property evaluation and implement classical gas dynamics correlations for pipeline flow. The tools handle both idealized thermodynamic processes (isentropic, isothermal, polytropic) and practical empirical formulas developed for natural gas transmission.
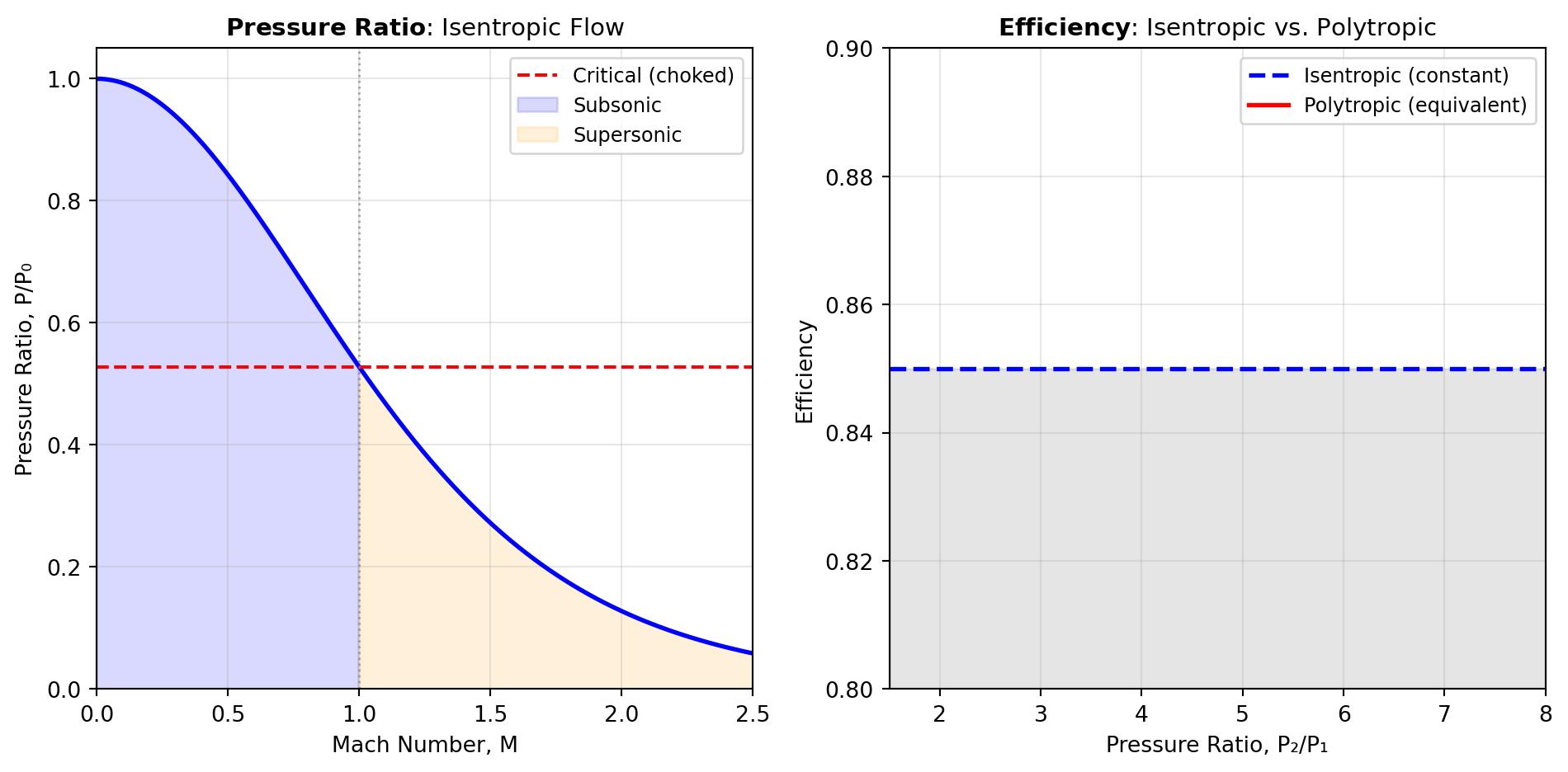
Thermodynamic Processes govern how gases behave during compression, expansion, and flow through varying areas. Isentropic processes assume reversible adiabatic conditions—ideal for analyzing turbomachinery and nozzles where heat transfer is negligible and losses are small. The ISENTROPIC_WORK, ISENTROPIC_T_RISE, and ISENTROPIC_EFF tools quantify compression work, temperature changes, and efficiency conversions for compressors and turbines. Isothermal processes assume constant temperature—applicable to slow compression with heat removal or long pipelines where gas temperature equilibrates with surroundings. The ISOTHERMAL_WORK and ISOTHERMAL_GAS tools handle these conditions. Polytropic processes represent real compression with some heat transfer, captured by the POLYTROPIC_EXP tool which relates efficiency to the polytropic exponent.
Stagnation Properties measure total energy available in a flow by accounting for both static conditions and kinetic energy. P_STAGNATION and T_STAGNATION convert between static and stagnation states, essential for performance analysis of compressors, turbines, and wind tunnels. The STAGNATION_ENERGY quantifies the enthalpy rise from velocity, while T_STAG_IDEAL provides the theoretical temperature rise.
Critical Flow Conditions occur when flow reaches Mach 1, establishing maximum flow rates that cannot increase regardless of further downstream pressure reduction—a phenomenon called choking. The IS_CHOKED_FLOW tool determines whether flow has reached critical conditions based on pressure ratio, while P_CRITICAL_FLOW and T_CRITICAL_FLOW calculate the exact pressure and temperature at the sonic condition. This behavior governs relief valve sizing, nozzle design, and pipeline capacity limits.
Pipeline Flow Formulas provide empirical correlations for natural gas transmission developed from extensive field data. These formulas account for friction, compressibility, and non-ideal gas behavior in long pipelines. WEYMOUTH_FLOW applies to large-diameter, high-pressure transmission lines with turbulent flow. PANHANDLE_A and PANHANDLE_B suit partially turbulent flow in moderate-diameter lines, with Panhandle B providing better accuracy for modern smooth pipes. FRITZSCHE_FLOW, MULLER_FLOW, and IGT_FLOW offer alternative formulations calibrated to specific pipeline conditions and gas properties.
Figure 1 illustrates the relationship between pressure ratio and Mach number in isentropic flow, and the efficiency conversions between isentropic and polytropic processes in compression.

Tools
| Tool | Description |
|---|---|
| FRITZSCHE_FLOW | Calculate gas flow rate using the Fritzsche formula. |
| IGT_FLOW | Calculate gas flow rate using the IGT (Institute of Gas Technology) formula. |
| IS_CHOKED_FLOW | Determine if a flow is choked (critical) based on pressure ratio. |
| ISENTROPIC_EFF | Convert between isentropic and polytropic efficiency for compression. |
| ISENTROPIC_T_RISE | Calculate the temperature rise for isentropic compression or expansion. |
| ISENTROPIC_WORK | Calculate work of compression or expansion for a gas in an isentropic process. |
| ISOTHERMAL_GAS | Calculate mass flow rate for isothermal compressible gas flow in a pipe. |
| ISOTHERMAL_WORK | Calculate work of compression or expansion for a gas in an isothermal process. |
| MULLER_FLOW | Calculate gas flow rate using the Muller formula. |
| P_CRITICAL_FLOW | Calculate critical flow pressure for a fluid at Mach 1. |
| P_STAGNATION | Calculate stagnation pressure from static conditions. |
| PANHANDLE_A | Calculate gas flow rate in a pipeline using the Panhandle A formula. |
| PANHANDLE_B | Calculate gas flow rate in a pipeline using the Panhandle B formula. |
| POLYTROPIC_EXP | Calculate polytropic exponent or polytropic efficiency for compression. |
| STAGNATION_ENERGY | Calculate the increase in enthalpy due to fluid velocity. |
| T_CRITICAL_FLOW | Calculate critical flow temperature for a fluid at Mach 1. |
| T_STAG_IDEAL | Calculate ideal stagnation temperature from velocity and heat capacity. |
| T_STAGNATION | Calculate stagnation temperature from pressure ratio. |
| WEYMOUTH_FLOW | Calculate gas flow rate in a pipeline using the Weymouth formula. |